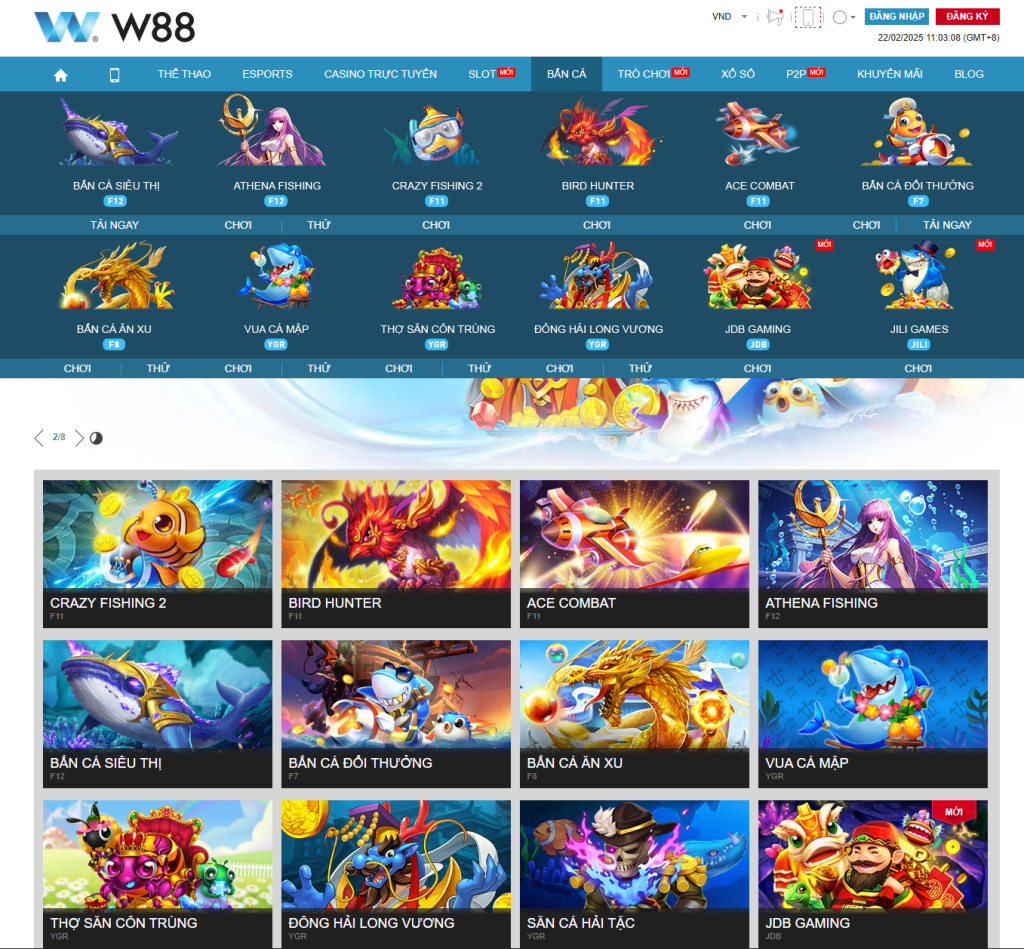
Trải nghiệm ngay game Bắn Cá H5 đổi thưởng 2025 với đồ họa siêu đẹp, săn cá cực đã, và đổi thưởng tiền thật nhanh chóng. Không cần tải app, chơi trực tiếp trên mọi thiết bị! 💎 Nhận ngay quà tặng tân thủ, tham gia sự kiện nổ hũ siêu khủng, rút tiền chỉ trong 1 phút.
Không cần tải ứng dụng, chơi mọi lúc mọi nơi, hỗ trợ điện thoại và máy tính.
Bắn Cá W88 – Game Hay, Nổ Hũ Lớn, Rút Tiền 1 Phút
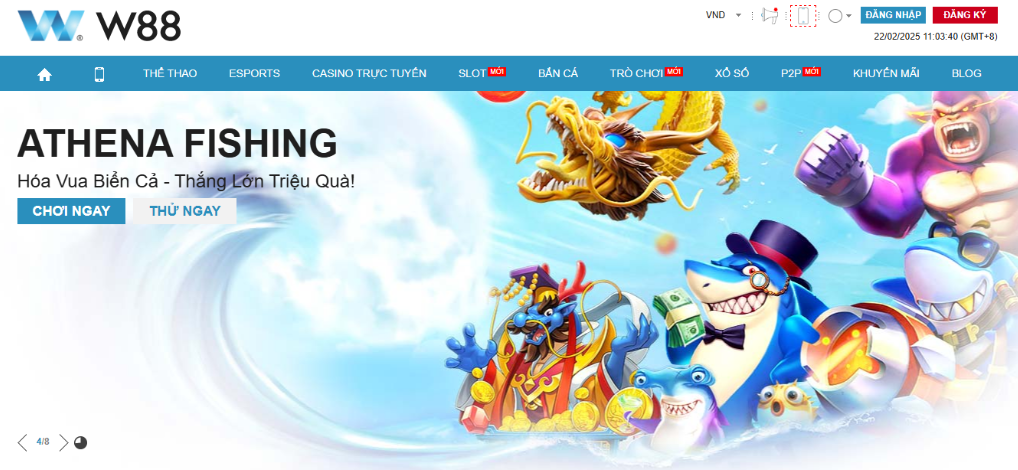
1. Bắn Cá W88 là gì? Vì sao game này lại hot?
Bắn Cá W88 là một tựa game giải trí trực tuyến, nơi người chơi có thể săn cá để nhận thưởng bằng tiền thật. Nhờ cơ chế đơn giản, giao diện bắt mắt và khả năng đổi thưởng nhanh, trò chơi này đã thu hút hàng triệu người tham gia.
🔥 Vì sao Bắn Cá W88 được yêu thích?
- Không cần tải ứng dụng: Chơi trực tiếp trên trình duyệt, không tốn dung lượng.
- Nhiều mức cược đa dạng: Phù hợp với cả người chơi mới và cao thủ.
- Rút tiền siêu tốc: Hỗ trợ nhiều phương thức thanh toán, tiền về trong vòng 5 phút.
- Đồ họa sinh động: Trải nghiệm hình ảnh 3D sắc nét, âm thanh sống động.
- Cộng đồng đông đảo: Kết nối với nhiều người chơi khác nhau, tăng trải nghiệm giải trí.
2. Hướng dẫn cách chơi Bắn Cá W88 chi tiết
📌 Để ý
Nếu xảy ra lỗi như hình bên dưới thì nhấn vào để làm mới trang để vào. Nếu không thể nhập nhiều lần làm mới (chức năng phân bổ dòng tối ưu)
📌 Bước 1: Đăng ký tài khoản
Truy cập trang web game, chọn “Đăng ký”, nhập thông tin cần thiết và xác nhận email.
📌 Bước 2: Nạp tiền vào tài khoản
Hệ thống hỗ trợ nhiều phương thức như ví điện tử, thẻ ngân hàng, thẻ cào điện thoại.
📌 Bước 3: Lựa chọn phòng chơi phù hợp
Các phòng chơi thường được chia theo mức cược: Tân thủ, Chuyên nghiệp, VIP.
📌 Bước 4: Sử dụng vũ khí hiệu quả
Mỗi loại súng có ưu nhược điểm khác nhau:
| Loại súng | Sát thương | Tốc độ bắn | Giá mua |
|---|---|---|---|
| Súng đơn | Thấp | Nhanh | Miễn phí |
| Súng đôi | Trung bình | Trung bình | 10.000 VNĐ |
| Súng laze | Cao | Chậm | 50.000 VNĐ |
📌 Bước 5: Rút tiền thưởng
Sau khi tích lũy điểm, người chơi có thể đổi thưởng và rút tiền về tài khoản ngân hàng trong vòng 5-10 phút.
3. So sánh Bắn Cá W88 với các game đổi thưởng khác
| Tiêu chí | Bắn Cá W88 | Game đổi thưởng khác |
| Tốc độ rút tiền | 5-10 phút | 24 giờ hoặc hơn |
| Giao diện | Mượt, sắc nét | Đôi khi giật lag |
| Tỷ lệ thắng | Cao hơn | Thấp hơn |
| Hỗ trợ nền tảng | Web, mobile | Chủ yếu là app |
👉 Kết luận: Bắn Cá W88 chiếm ưu thế về tốc độ rút tiền và trải nghiệm mượt mà.
4. Những sai lầm phổ biến khi chơi Bắn Cá W88
⚠ Lưu ý những điều sau để tránh mất tiền oan!
❌ Chỉ bắn cá lớn: Cá lớn cho thưởng cao nhưng khó tiêu diệt, cần có chiến thuật hợp lý.
❌ Không quản lý vốn: Hãy đặt ngân sách và tuân thủ nguyên tắc chơi an toàn.
❌ Bỏ qua các sự kiện khuyến mãi: Nhiều nhà cái có chương trình tặng tiền nạp, giúp bạn tăng vốn chơi.
5. Câu chuyện thực tế: Chúng tôi đã kiếm tiền từ Bắn Cá W88 thế nào?
Năm 2025, chúng tôi đã thử nghiệm một chiến lược chơi Bắn Cá W88 trong 1 tháng. Kết quả:
- Vốn đầu tư ban đầu: 1.000.000 VNĐ
- Lợi nhuận sau 30 ngày: 4.200.000 VNĐ
- Tỷ lệ thắng trung bình: 78%
📌 Chiến lược chúng tôi áp dụng:
- Sử dụng súng đôi để tối ưu sát thương.
- Chỉ bắn cá có giá trị từ trung bình trở lên.
- Kiểm soát ngân sách chặt chẽ.
6. Checklist: Bạn đã sẵn sàng kiếm tiền từ Bắn Cá W88?
✅ Chọn đúng nền tảng game uy tín.
✅ Đăng ký tài khoản và xác minh thông tin.
✅ Nạp tiền một cách an toàn.
✅ Tìm hiểu cách dùng súng hiệu quả.
✅ Lập kế hoạch quản lý vốn chặt chẽ.
✅ Theo dõi sự kiện khuyến mãi để tối ưu lợi nhuận.
✅ Kiểm soát cảm xúc, không chạy theo thua lỗ.
👉 Nếu bạn đã hoàn thành tất cả các bước trên, hãy bắt đầu chơi ngay và tận hưởng trải nghiệm Bắn Cá W88 cực đã! Đừng bỏ lỡ cơ hội tham gia ngay tại W88 – nhà cái uy tín hàng đầu!